Variograms

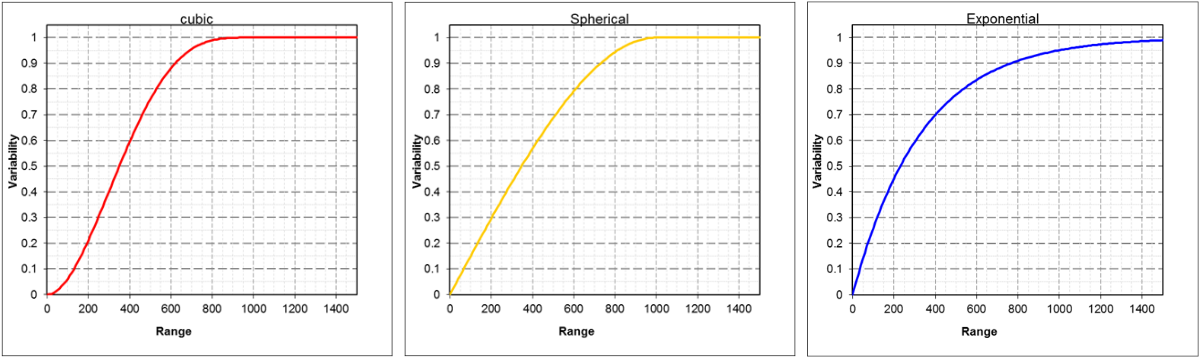
Cubic variogram

When \(h \leq a\)
$$
\gamma (h) = C \left[ 7 \left( \frac{h}{a} \right)^2 – \frac{35}{4} \left( \frac{h}{a} \right)^3 + \frac{7}{2} \left( \frac{h}{a} \right)^5 – \frac{3}{4} \left( \frac{h}{a} \right)^7 \right]
$$

When \(h > a\)
$$
\gamma (h) = C
$$

Where:

• \(h\) = separation distance
• \(C\) = sill – nugget
• \(a\) = effective range

Spherical variogram

When \(h < a\) $$ \gamma (h) = C \left[ \frac{3}{2} \left( \frac{h}{a} \right) - \frac{1}{2} \left( - \frac{h}{a} \right)^3 \right] $$

When \(h \geq a\)
$$
\gamma (h) = C
$$

Where:

• \(h\) = separation distance
• \(C\) = sill – nugget
• \(a\) = effective range

Exponential variogram

Exponential variogram

$$
\gamma (h) = C \left[ 1 – exp \left( – \, \frac{\delta h}{a} \right) \right]
$$

Where:

• \(h\) = separation distance
• \(C\) = sill – nugget
• \(a\) = effective range, defined as the distance at which \((h)\) = 0.95 \(C\)
• \( \delta\) = 2.996 = scaling factor