| Parameters | $$-\infty < min < mode < max < +\infty $$ |
| Support | $$x \in \mathbb{R} \quad and \quad p \in \:]0,1 [$$ |
|
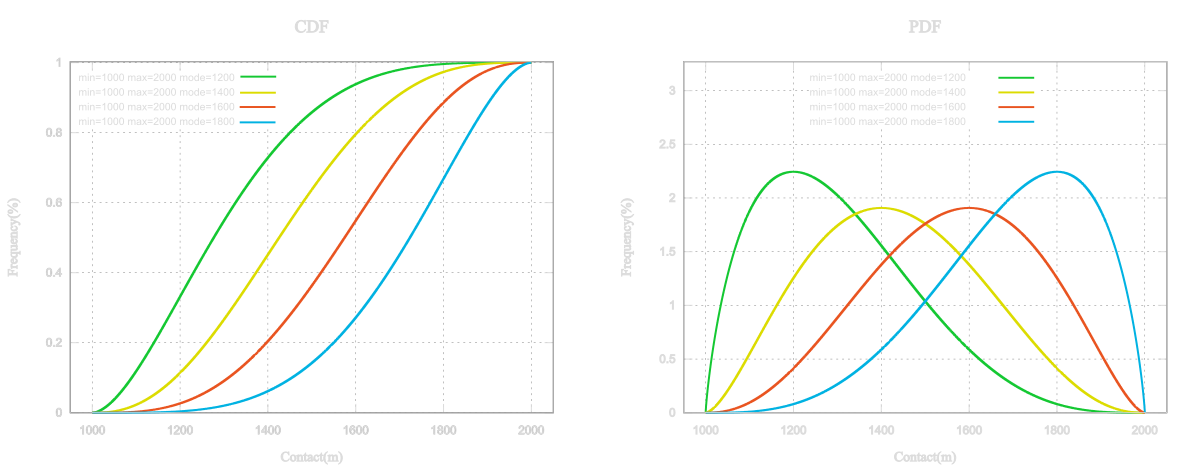
$$ PDF = \frac{x^{(a-1)} (1-x)^{(b-1)}}{ B(a,b)} $$ $$ with \qquad B(a,b)= \frac{\Gamma(a)+ \Gamma(b)}{ \Gamma(a+b)} , \qquad the \, Beta \, function $$ $$ with \qquad \Gamma(.)= Gamma \, function $$ $$ with \qquad \left\{ \begin{array}{rl} a = 1+4 \left( \frac{mode-min}{(max-min)} \right),\\ b = 1+4 \left( \frac{max-mode}{(max-min)} \right), \end{array} \right. \qquad according \, to \, PERT \, method $$ |
|
| CDF |
$$ CDF = I_{x}(a,b)$$ $$ with \qquad I_{x}(a,b)= \frac{B(x;a,b)}{ B(a,b)} , \qquad the \, Incomplete \, beta \, function $$ $$ with \qquad \left\{ \begin{array}{rl} a = 1+4 \left( \frac{mode-min}{(max-min)} \right),\\ b = 1+4 \left( \frac{max-mode}{(max-min)} \right), \end{array} \right. \qquad according \, to \, PERT \, method $$ |
| CDF-1 |
$$ CDF^{-1} = I^{-1}_{x}(a,b)$$ $$ with \qquad I^{-1}_{p}(a,b) , \qquad the \, Inverse \, incomplete \, beta \, function $$ |

Become an expert at using Udomore® softwares