| Parameters | $$-\infty < min < mode < max < +\infty $$ |
| Support | $$x \in [min,max ] \quad and \quad p \in \:]0,1 [$$ |
|
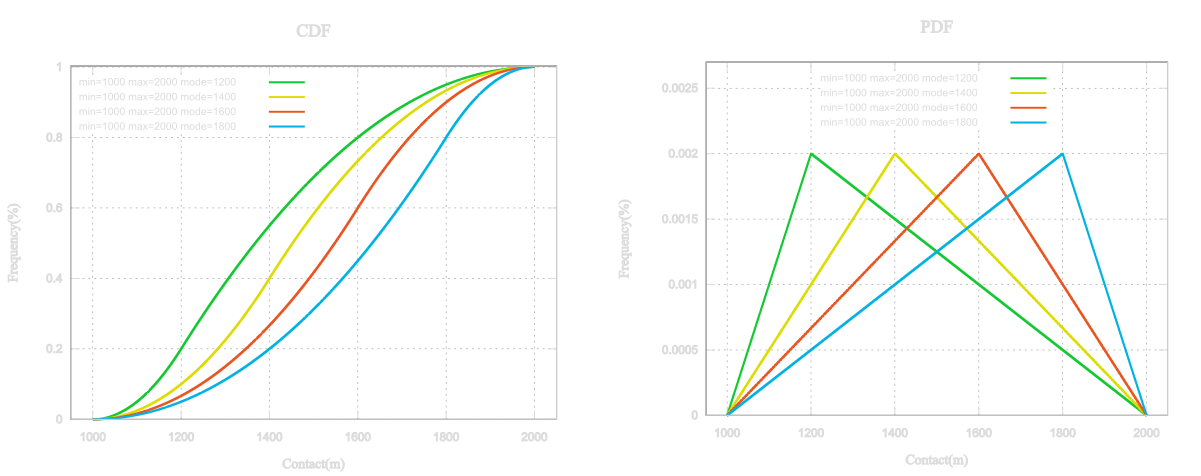
$$ PDF = \left\{ \begin{array}{rl} \frac{0.5}{(mode-min)}, &\mbox{ for min $ \le x \le $ mode}\\ \frac{0.5}{(max-mode)}, &\mbox{ for mode $< x \le $ max} \end{array} \right. $$ |
|
| CDF |
$$ CDF = \left\{ \begin{array}{rl} 0.5 \times \left( \frac{x-min}{(mode-min)} \right) \quad, &\mbox{ for min $\le x \le$ mode}\\ 0.5 \times \left[ \left(\frac{x-min}{(max-mode)} \right)+1 \right], &\mbox{ for mode $< x \le$ max} \end{array} \right. $$ |
| CDF-1 |
$$ CDF^{-1} = \left\{ \begin{array}{rl} min \qquad \qquad \quad, &\mbox{ for p $< $ 0}\\ min + (2 \times p) (mode-min), &\mbox{ for $0\le p <0.5$ }\\ mode+ (2 \times p) (max-mode), &\mbox{ for $0.5\le p \le1$ }\\ max \qquad \qquad \quad, &\mbox{ for p > 1} \end{array} \right. $$ |

Become an expert at using Udomore® software