| Parameters |
$$µ \in \mathbb{R} $$ $$\sigma^2>0$$ |
| Support | $$x \in [\mathbb{R}] \quad and \quad p \in \:]0,1 [$$ |
|
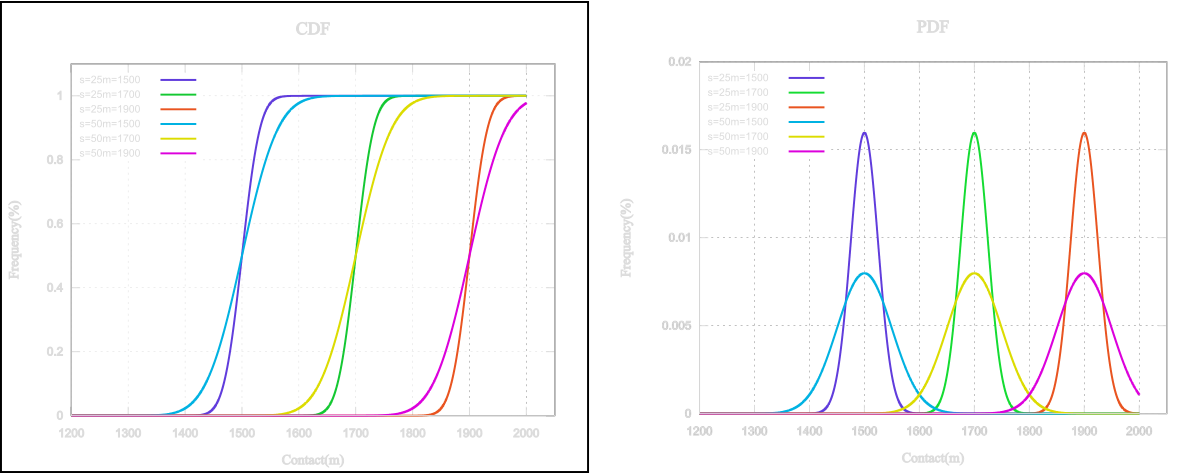
$$ PDF = \frac{1}{ \sqrt{2 \times \sigma^2 \pi }} e^{ \frac { (x-µ)^2 } { 2 \sigma^2 } } $$ |
|
| CDF |
$$ CDF = \frac {1}{2} \left[ 1 + erf \left( \frac{x-µ}{\sigma \sqrt{2}} \right) \right] $$ |
| CDF-1 | $$ CDF^{-1} = \sigma \times \sqrt {2} er f^{-1} (2 \times p) + µ $$ |

Become an expert at using Udomore® software